L'algorithme BM25 en pratique - 2^e partie : l'algorithme BM25 et ses variables

Voici la deuxième publication consacrée à l'algorithme BM25 en pratique dans cette série de trois articles sur le classement par similarité (pertinence). Si vous ne l'avez pas encore fait, vous pouvez lire la 1^re partie expliquant en quoi les partitions influent sur le score de pertinence dans Elasticsearch.

L'algorithme BM25

Je vais tenter de ne pas abuser des explications mathématiques pour vous parler du sujet de cet article. Cependant, dans cette partie, nous étudions la structure de la formule de l'algorithme BM25 afin d'en comprendre le fonctionnement. Observons tout d'abord la formule. Ensuite, j'aborderai chacun de ces composants séparément afin de les rendre compréhensibles.

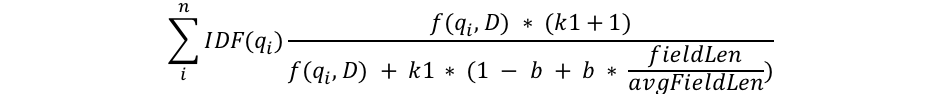
Nous remarquons la présence de composants courants, comme q_i, IDF(q_i), f(q_i,D), k1 et b, mais aussi un composant lié à la longueur de champ. Voici à quoi chaque composant correspond :

1. q_i est le i^e terme de requête.
   
   Par exemple, si je cherche le mot "shane", la requête comprend un seul terme. Par conséquent, q₀ représente "shane". Si je cherche "shane connelly" en anglais, Elasticsearch identifie l'espace entre ces mots et génère des tokens pour cette requête en 2 termes : q₀ représente "shane" et q₁ "connelly". Ces termes sont connectés aux autres éléments de l'équation afin de tous les récapituler.
2. IDF(g_i) est la fréquence inverse de document du i^e terme de requête.
   
   Si vous avez déjà travaillé avec TF/IDF, vous connaissez sans doute le concept d'IDF. Si ce n'est pas le cas, ce n'est pas grave. (Si c'est bien le cas, remarquez la différence entre la formule IDF dans le schéma TF/IDF et l'IDF dans l'algorithme BM25.) Le composant IDF de notre formule évalue la fréquence d'un terme dans l'ensemble des documents et "pénalise" les termes courants. Lucene/l'algorithme BM25 utilise la formule suivante pour cette partie.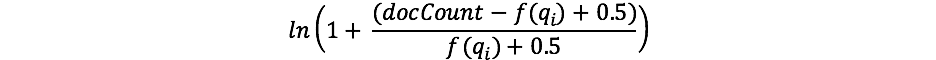
   
   
   Le composant docCount représente le nombre total de documents dotés d'une valeur pour le champ dans la partition (parmi les différentes partitions si vous utilisez search_type=dfs_query_then_fetch), et f(q_i) représente le nombre de documents qui contiennent le i^e terme de requête. Dans notre exemple, le terme "shane" apparaît dans les quatre documents. Par conséquent, pour le terme "shane", nous obtenons l'IDF("shane") suivant.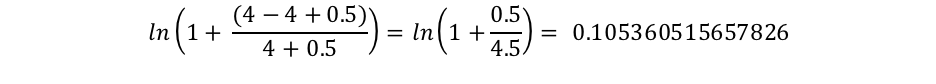
   
   
   Or, le terme "connelly" apparaît uniquement dans deux documents. Ainsi, nous obtenons l'IDF("connelly") suivant.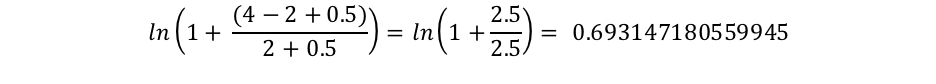
   
   
   Nous constatons que les requêtes contenant ces termes plus rares ("connelly" étant plus rare que "shane" dans notre corpus de quatre documents) sont dotées d'un effet multiplicateur plus élevé. Par conséquent, elles contribuent davantage au score final. Il y a une explication intuitive à cela : le terme "the" est susceptible d'apparaître dans quasiment chaque document rédigé en anglais. Ainsi, lorsque des internautes recherchent les mots "the elephant", le terme "elephant" est probablement plus important (et il serait logique qu'il contribue davantage au score) que le terme "the" (présent dans la quasi-totalité des documents).
   
3. Nous constatons que la longueur du champ est divisée par la longueur de champ moyenne dans le dénominateur de la manière suivante : fieldLen/avgFieldLen.
   
   Une autre représentation consiste à déterminer la longueur d'un document par rapport à la longueur de document moyenne. Si un document est plus long que la moyenne, le dénominateur est plus élevé (ce qui diminue le score). En revanche, si le document est plus court que la moyenne, le dénominateur est plus bas (ce qui augmente le score). Il convient de noter que l'implémentation de la longueur de champ dans Elasticsearch se fonde sur le nombre de termes (par rapport à un autre élément, comme la longueur des caractères). Voilà ce qui était expliqué dans l'article originel sur l'algorithme BM25. Toutefois, nous disposons d'un indicateur spécial (discount_overlaps) pour gérer les synonymes, notamment si vous le souhaitez. Il faut comprendre que plus les documents contiennent de termes (tout au moins ceux qui ne correspondent pas à la requête), plus leur score est bas. À nouveau, il existe une explication intuitive : si un document est composé de 300 pages et cite mon nom une seule fois, il est peu probable que ce texte me concerne, à l'instar d'un court tweet me mentionnant une seule fois.
4. Le dénominateur comprend une variable b qui est multipliée par l'équation de la longueur du champ mentionnée ci-dessus. Si b est plus élevée, les effets de la longueur du document par rapport à la longueur moyenne sont davantage amplifiés. Pour le comprendre en pratique, imaginez que vous configuriez b sur 0, l'effet du rapport de longueur serait entièrement annulé et la longueur du document n'aurait aucun rapport avec le score. Par défaut, b a une valeur de 0,75 dans Elasticsearch.
5. Enfin, deux composants du score apparaissent dans le numérateur et le dénominateur, à savoir k1 et f(q_i,D). Étant donné qu'ils apparaissent des deux côtés de l'équation, il est difficile de comprendre leur rôle simplement en regardant la formule. Examinons-les rapidement.
   1. f(q_i,D) correspond au nombre de fois que le i^e terme de requête apparaît dans le document D. Dans tous ces documents, f("shane",D) est 1, mais f("connelly",D) varie : 1 se trouve dans les documents 3 et 4, et 0 dans les documents 1 et 2. S'il existait un 5 ^e document contenant les mots "shane shane", il comprend f("shane",D) avec une valeur de 2. Nous constatons que f(q_i,D) apparaît dans le numérateur et le dénominateur, mais aussi la présence d'un facteur "k1" spécial que nous allons étudier ensuite. Concernant f(q_i,D), plus le ou les termes de requête apparaissent dans un document, plus le score sera élevé. Il existe une explication intuitive : un document dans lequel notre nom est mentionné de nombreuses fois est plus susceptible de parler de nous par rapport à un document où notre nom est cité une seule fois.
   2. k1 est une variable qui aide à déterminer les caractéristiques de saturation de la fréquence des termes. Elle limite la mesure dans laquelle un seul terme de requête peut influer sur le score d'un document donné. Dans ce but, elle se rapproche d'une asymptote. Voici une comparaison de l'algorithme BM25 et de TF/IDF.
      
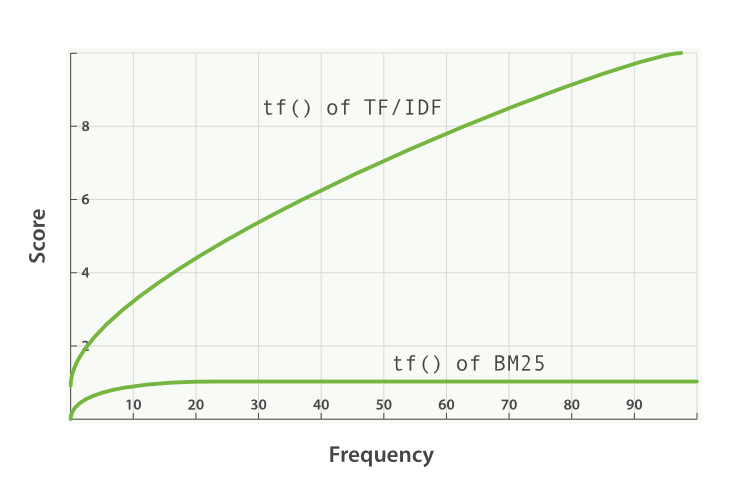
      Une valeur k1 supérieure/inférieure signifie que la courbe "tf() of BM25" évolue. Ainsi, elle influe sur la manière dont les termes apparaissant un nombre de fois supplémentaire augmentent le score. Selon une interprétation de k1, pour les documents d'une longueur moyenne, il s'agit de la valeur de la fréquence d'un terme qui donne un score correspondant à la moitié du score maximal pour le terme concerné. La courbe de l'impact de tf sur le score augmente rapidement lorsque tf() ≤ k1 et diminue de plus en plus lorsque tf() > k1.
      
      Toujours avec le même exemple, grâce à k1, nous contrôlons la réponse à la question relative à la contribution au score de l'ajout d'un deuxième "shane" dans le document en comparant le premier ou le troisième au deuxième. Lorsque k1 est plus élevé, le score pour chaque terme peut continuer à augmenter de manière relative lorsque ce terme apparaît plusieurs fois. Si k1 a une valeur de 0, cela signifie que tous les éléments, sauf IDF(q_i), s'annuleraient. Par défaut, k1 a une valeur de 1,2 dans Elasticsearch.

Révision de notre recherche à la lumière de nos nouvelles connaissances

Nous supprimerons l'index people et le recréerons avec une seule partition afin de ne pas devoir utiliser search_type=dfs_query_then_fetch. Nous testerons nos connaissances en configurant trois index : un index comprend la valeur de k1 configurée sur 0 et de b sur 0,5 ; un deuxième index (people2) comprend la valeur de b configurée sur 0 et de k1 sur 10 ; enfin, un troisième index (people3) comprend une valeur de b configurée sur 1 et de k1 configurée sur 5.

DELETE people
PUT people
{
  "settings": {
    "number_of_shards": 1,
    "index" : {
        "similarity" : {
          "default" : {
            "type" : "BM25",
            "b": 0.5,
            "k1": 0
          }
        }
    }
  }
}
PUT people2
{
  "settings": {
    "number_of_shards": 1,
    "index" : {
        "similarity" : {
          "default" : {
            "type" : "BM25",
            "b": 0,
            "k1": 10
          }
        }
    }
  }
}
PUT people3
{
  "settings": {
    "number_of_shards": 1,
    "index" : {
        "similarity" : {
          "default" : {
            "type" : "BM25",
            "b": 1,
            "k1": 5
          }
        }
    }
  }
}

Ensuite, nous ajouterons quelques documents à ces trois index.

POST people/_doc/_bulk
{ "index": { "_id": "1" } }
{ "title": "Shane" }
{ "index": { "_id": "2" } }
{ "title": "Shane C" }
{ "index": { "_id": "3" } }
{ "title": "Shane P Connelly" }
{ "index": { "_id": "4" } }
{ "title": "Shane Connelly" }
{ "index": { "_id": "5" } }
{ "title": "Shane Shane Connelly Connelly" }
{ "index": { "_id": "6" } }
{ "title": "Shane Shane Shane Connelly Connelly Connelly" }
POST people2/_doc/_bulk
{ "index": { "_id": "1" } }
{ "title": "Shane" }
{ "index": { "_id": "2" } }
{ "title": "Shane C" }
{ "index": { "_id": "3" } }
{ "title": "Shane P Connelly" }
{ "index": { "_id": "4" } }
{ "title": "Shane Connelly" }
{ "index": { "_id": "5" } }
{ "title": "Shane Shane Connelly Connelly" }
{ "index": { "_id": "6" } }
{ "title": "Shane Shane Shane Connelly Connelly Connelly" }
POST people3/_doc/_bulk
{ "index": { "_id": "1" } }
{ "title": "Shane" }
{ "index": { "_id": "2" } }
{ "title": "Shane C" }
{ "index": { "_id": "3" } }
{ "title": "Shane P Connelly" }
{ "index": { "_id": "4" } }
{ "title": "Shane Connelly" }
{ "index": { "_id": "5" } }
{ "title": "Shane Shane Connelly Connelly" }
{ "index": { "_id": "6" } }
{ "title": "Shane Shane Shane Connelly Connelly Connelly" }

Désormais, lorsque nous procédons comme suit :

GET /fr/people/_search
{
  "query": {
    "match": {
      "title": "shane"
    }
  }
}

Nous constatons que, dans l'index people, l'ensemble des documents a un score de 0,074107975. Cela correspond à notre compréhension de la configuration de k1 sur 0 : seul l'IDF du terme de recherche est important pour le score.

À présent, vérifions l'index people2, qui comprend une valeur de b égale à 0 et de k1 égale à 10.

GET /fr/people2/_search
{
  "query": {
    "match": {
      "title": "shane"
    }
  }
}

Deux enseignements doivent être tirés des résultats de cette recherche.

Tout d'abord, nous pouvons considérer les scores comme simplement classés en fonction du nombre d'occurrences du mot "shane". Les documents 1, 2, 3 et 4 contiennent tous une occurrence du mot "shane". Par conséquent, ils ont le même score de 0,074107975. Le document 5 comprend deux occurrences de "shane". Ainsi, il a un score plus élevé (0,13586462) étant donné que f("shane",D5) est égal à 2, et le document 6 a à nouveau un score plus élevé (0,18812023) comme f("shane",D6) est égal à 3. Ce résultat correspond à notre intuition concernant la configuration de b sur 0 dans l'index people2 : la longueur (ou le nombre total de termes dans le document) n'influe pas sur le score, uniquement sur le nombre et la pertinence des termes correspondants.

Second enseignement à tirer, les différences entre ces scores ne sont pas linéaires, même si elles semblent vraiment l'être avec ces six documents.

• La différence de score entre aucune occurrence de notre terme de recherche et la première occurrence est 0,074107975.
• La différence de score entre ajouter une deuxième occurrence de notre terme de recherche et la première occurrence est 0,13586462 - 0,074107975 = 0,061756645.
• La différence de score entre ajouter une troisième occurrence de notre terme de recherche et la deuxième occurrence est 0,18812023 - 0,13586462 = 0,05225561.

La différence 0,074107975 est très proche de 0,061756645, qui est très proche de 0,05225561. Toutefois, le score diminue de manière évidente. Ces différences semblent presque linéaires, car k1 est vaste. Nous pouvons toutefois constater que le score n'augmente pas de manière linéaire lorsque des occurrences sont ajoutées. Si c'était le cas, nous devrions obtenir la même différence à chaque ajout de terme. Nous reviendrons sur cette idée après avoir étudié l'index people3.

À présent, vérifions l'index people3, qui comprend une valeur de k1 égale à 5 et de b égale à 1.

GET /fr/people3/_search
{
  "query": {
    "match": {
      "title": "shane"
    }
  }
}

Nous obtenons les résultats suivants.

"hits": [
      {
        "_index": "people3",
        "_type": "_doc",
        "_id": "1",
        "_score": 0.16674294,
        "_source": {
          "title": "Shane"
        }
      },
      {
        "_index": "people3",
        "_type": "_doc",
        "_id": "6",
        "_score": 0.10261105,
        "_source": {
          "title": "Shane Shane Shane Connelly Connelly Connelly"
        }
      },
      {
        "_index": "people3",
        "_type": "_doc",
        "_id": "2",
        "_score": 0.102611035,
        "_source": {
          "title": "Shane C"
        }
      },
      {
        "_index": "people3",
        "_type": "_doc",
        "_id": "4",
        "_score": 0.102611035,
        "_source": {
          "title": "Shane Connelly"
        }
      },
      {
        "_index": "people3",
        "_type": "_doc",
        "_id": "5",
        "_score": 0.102611035,
        "_source": {
          "title": "Shane Shane Connelly Connelly"
        }
      },
      {
        "_index": "people3",
        "_type": "_doc",
        "_id": "3",
        "_score": 0.074107975,
        "_source": {
          "title": "Shane P Connelly"
        }
      }
    ]

Dans l'index people3, nous constatons que le taux de termes correspondants ("shane") par rapport aux termes non correspondants est la seule chose influant sur le score relatif. Ainsi, les documents similaires au document 3, qui contient uniquement un terme correspondant sur trois, ont un score inférieur aux documents 2, 4, 5 et 6, qui correspondent tous exactement à la moitié des termes et ont tous un score inférieur au document 1 qui correspond exactement au document.

De nouveau, nous remarquons une très grande différence entre les documents ayant le score le plus élevé et ceux ayant le score le plus bas dans les index people2 et people3. Ce résultat est (à nouveau) dû à une valeur plus élevée pour k1. Comme nouvel exercice, essayez de supprimer les index people2/people3 et de les reconfigurer avec une valeur similaire à k1 égale à 0,01. Vous constaterez des scores inférieurs entre les documents contenant moins d'occurrences. Lorsque b est égal à 0 et k1 est égal à 0,01 :

• La différence de score entre aucune occurrence de notre terme de recherche et la première occurrence est 0,074107975.
• La différence de score entre ajouter une deuxième occurrence de notre terme de recherche et la première occurrence est 0,074476674 - 0,074107975 = 0,000368699.
• La différence de score entre ajouter une troisième occurrence de notre terme de recherche et la deuxième occurrence est 0,07460038 - 0,074476674 = 0,000123706.

Par conséquent, lorsque k1 est égal à 0,01, l'influence du score de chaque occurrence supplémentaire diminue bien plus rapidement par rapport à une valeur de k1 égale à 5 ou de k1 égale à 10. La 4^e occurrence représenterait un ajout bien inférieur au score par rapport à la 3^e et ainsi de suite. En d'autres termes, les scores des termes sont saturés bien plus rapidement qu'avec les valeurs de k1 inférieures, comme nous nous y attendions.

Nous espérons que ces explications vous aideront à comprendre l'influence de ces paramètres sur plusieurs ensembles de documents. Grâce à nos nouvelles connaissances, nous pouvons découvrir comment choisir des valeurs b et k1 appropriées, mais aussi comment Elasticsearch fournit des outils pour comprendre les scores et reproduire l'approche utilisée.

Poursuivons la série avec la Troisième partie : éléments à envisager pour choisir les valeurs b et k1 dans Elasticsearch.