kNNとは?
k近傍法の定義
kNNまたはk近傍法アルゴリズムとは、近接性を利用する機械学習アルゴリズムです。1つのデータポイントを、予測を行うためにトレーニングされ記憶された一連のデータセットと比較します。インスタンスベースのこの学習方法により、kNNは「怠惰学習」の一派とみなされ、分類問題や回帰問題を処理できるアルゴリズムとなっています。kNNは、「類は友を呼ぶ」、つまり類似するポイントは互いに近接するという前提で機能します。
分類アルゴリズムとしてのkNNでは、新しいデータポイントを近傍の多数派セットに割り当てます。回帰アルゴリズムとしてのkNNでは、クエリポイントに最も近い値の平均に基づいて予測を行います。
kNNは、教師あり学習アルゴリズムです。kNNの「k」は分類問題または回帰問題で考慮する最近傍の数を表し、「NN」はk個の最近傍を表します。
kNNアルゴリズムの沿革
kNNの原型は、米軍が実施した調査に関連して、1951年にイブリン・フィックス氏とジョセフ・ホッジス氏によって誕生しました1。2人が発表した論文は、ノンパラメトリック分類法による判別分析に関するものでした。1967年には、トーマス・カバー氏とピーター・ハート氏がノンパラメトリック分類法を拡張し、「Nearest Neighbor Pattern Classification(最近傍パターン分類)」という論文を発表します2。それから約20年後、このアルゴリズムを洗練させたジェームズ・ケラー氏により、エラー率の低い「ファジーKNN」が開発されます3。
現在、遺伝学から金融やカスタマーサービスに至るまで、大半の分野に応用がきくkNNアルゴリズムは、最も広範に使用されるアルゴリズムになっています。
kNNの仕組み
kNNアルゴリズムは、教師あり学習アルゴリズムとして機能します。つまり、トレーニング用のデータセットが与えられ、それを記憶します。ラベル付きの入力データを手がかりにして、ラベルの付いていないデータが与えられたときに適切な結果を出力できる機能を学習します。
これにより、アルゴリズムは分類問題や回帰問題を解けるようになります。kNNの計算はトレーニング中ではなくクエリ中に行われますが、データストレージに関する重要な要件があるため、メモリーに大きく依存します。
分類問題では、kNNアルゴリズムは多数決ルールに基づいて分類ラベルを割り当てます。つまり、特定のデータポイントの周囲に最も多く存在するラベルが使用されます。別の表現をすると、分類問題では最近傍の最頻値が出力されます。
多数決と相対多数決の違い
多数決では、50%を超えるものが多数派とみなされます。これは、考慮するラベルが2種類である場合に適用されます。他方、相対多数決は考慮するラベルが複数ある場合に適用されます。たとえばラベルが3つの場合、33.3%を超えるものを多数派とみなすことができ、予測が提供されます。それゆえ、kNNにおける最頻値の定義としては、相対多数決と表現する方が正確です。
この違いをイラストで表現するなら、次のようになります。
ラベルが2種類の場合
Y: 🎉🎉🎉❤️❤️❤️❤️❤️
多数決:❤️
相対多数決:❤️
ラベルが複数種類の場合
Y:⏰⏰⏰ 💰 💰 💰 🏠 🏠 🏠 🏠
多数決:なし
相対多数決:🏠
回帰問題では、分類の予測に最近傍の平均値が使われます。回帰問題では、クエリに対して実数が出力されます。
たとえば、誰かの体重を身長に基づいて予測するチャートを作成しているとすると、身長を表す値は独立変数ですが、体重を表す値は依存変数です。身長体重比の平均値を計算することで、誰かの体重(依存変数)を身長(独立変数)に基づいて推定できます。
kNNの距離メトリックを計算する4つの方法
kNNアルゴリズムでは、クエリポイントと他のデータポイント間の距離の決定が重要になります。距離メトリックを決定すると、決定境界が有効になります。これらの境界が、さまざまなデータポイントリージョンを作り出します。さまざまな方法が距離の計算に使用されます。
- ユークリッド距離は、最も一般的な距離尺度です。クエリポイントと測定対象となる他のポイントを結ぶ直線を測定します。
- マンハッタン距離も、よく使用される距離尺度です。2点間の絶対値を測定します。グリッドで表現され、しばしばタクシー幾何学とも呼ばれます。つまり、A地点(クエリポイント)からB地点(測定対象のポイント)までの移動経路を測定します。
- ミンコフスキー距離は、ユークリッド距離とマンハッタン距離のメトリックを一般化したものであり、他の距離メトリックの作成を可能にします。ノルム線型空間で計算されます。ミンコフスキー距離では、pが計算で使用される距離の種類を定義するパラメーターになります。pが1の場合、マンハッタン距離が使われます。pが2の場合、ユークリッド距離が使われます。
- ハミング距離は、オーバラップメトリックとも呼ばれ、ブールベクトルか文字列ベクトルと組み合わせて使用し、ベクトルが一致しない場所を特定します。別の表現をすると、同じ長さの2つの文字列間の距離を測定します。エラー検出コードやエラー修正コードで特に重宝します。
最適なk値の選び方
最適なk値(考慮する最近傍の数)を選択するためには、いくつかの値を試してみて、最も正確な予測が生成され、エラー数が最も少なくなるk値を探し出す必要があります。最適な値を決定するには、バランスの見極めがポイントになります。
- k値が小さいと予測が不安定になります。
例として、クエリポイントの周りに緑の点が2つ、赤い三角が1つある場合を考えてみましょう。k = 1にして、たまたま緑の点の1つがクエリポイントに最も近いポイントとなっていた場合、アルゴリズムは間違った予測を行い、緑の点がクエリに対する出力になります。k値が小さいと、分散が大きく(モデルがトレーニングデータに近すぎる状態)、複雑度が高く、バイアスが小さく(モデルが複雑でトレーニングデータによく適合している状態)なります。 - k値が大きいとノイズが多くなります。
k値を大きくすると、予測の精度が上がります。最頻値や平均値を計算するための材料が増えるからです。しかし、k値が大きすぎると分散が小さく、バイアスが大きく(モデルが複雑でなくトレーニングデータと乖離している状態)なります。
分散が大きいものとバイアスが大きいものの中間になるk値を見つけるのが理想です。また、分類分析で同点になるのを避けるために、kは奇数にすることが推奨されます。
適切なk値は、データセットと関連するものでもあります。その値を選択するには、N(トレーニングデータセット内のデータポイント数)の平方根を求めてみてください。交差検証法も、データセットに最適なkの値を選択するのに役立つかもしれません。
kNNアルゴリズムのメリット
「最もシンプルな」教師あり学習アルゴリズムと表現されることも多いkNNには、いくつかのメリットがあります。
- シンプル:kNNは、そのシンプルさと正確さゆえ、簡単に実装できます。そのため、データサイエンティストが最初に学ぶ分類器の1つとされることも少なくありません。
- 順応性:データセットに新しいトレーニング用サンプルが追加されると、すぐにkNNアルゴリズムは新しいトレーニング用データを反映して予測を調整します。
- プログラム作成の容易さ: kNNに必要なのは、k値と距離メトリックという、ほんの数個のハイパーパラメーターだけです。そのため、きわめて単純なアルゴリズムになっています。
加えて、kNNアルゴリズムではトレーニングデータが保存されるのでトレーニング時間が不要です。また、演算処理能力は予測を行うときだけ使用されます。
kNNの課題と制限
kNNアルゴリズムはシンプルですが、ある意味そのシンプルさゆえの一連の課題と制限も伴います。
- スケーリングが困難:kNNは多くのメモリとデータストレージを消費するため、ストレージに関連する費用が発生します。このメモリー依存度の高さは、アルゴリズムのコンピューティング負荷が高いということでもあり、翻って消費するリソースの多さも意味します。
- 次元の呪い:これはコンピューターサイエンスの世界で起きる現象を指しています。次元が増えて特徴値が増えると、トレーニング対象であるサンプルの固定セットに課題が生じるという問題です。言い換えれば、モデルのトレーニングデータがハイパースペースにおける次元の増加ペースについていけなくなるという問題です。これは、別の次元で、クエリポイントと類似するポイントの距離がどんどん離れることで、予測の正確さが低下することを意味します。
- 過剰適合: すでに説明したように、kの値はアルゴリズムの挙動に影響します。過剰適合が特に起こりがちなのが、kの値が小さすぎる場合です。kが小さすぎると、データへの過剰適合が起きる可能性があります。反対に、kが大きすぎると予測値の「平準化」が起きます。より広い領域に渡ってアルゴリズムによる値の平均化が起きるからです。
kNNのよくあるユースケース
シンプルさと正確さで知られるkNNアルゴリズムには、分類分析での使用を筆頭に、さまざまな用途があります。
- 関連性ランキング:kNNは、自然言語処理(NLP)アルゴリズムを使用してクエリと最も関連性が高い結果を判断します。
- 画像または動画の類似性検索:画像または動画の類似性検索:
- パターン認識:kNNを使用して、テキストや数字分類のパターンを識別できます。
- 金融:金融業界では、kNNを株式市場予測や為替レートなどのために使用できます。
- 製品の提案と推奨エンジン:Netflixを思い浮かべてみてください。「...をご覧になったあなたにおすすめ」といった類いの文を見かけるサイトでは、公然とかどうかは別として、推奨エンジンにkNNアルゴリズムが使われている可能性が高いと思われます。
- 医療:医薬品や医学の研究分野では、遺伝学でkNNアルゴリズムを使用して特定の遺伝子発現の可能性を計算できます。これにより、がん、心臓発作、その他の遺伝子疾患を、医者が予測できます。
- データの前処理:kNNアルゴリズムを使用すれば、データセット内の欠損値を推定できます。
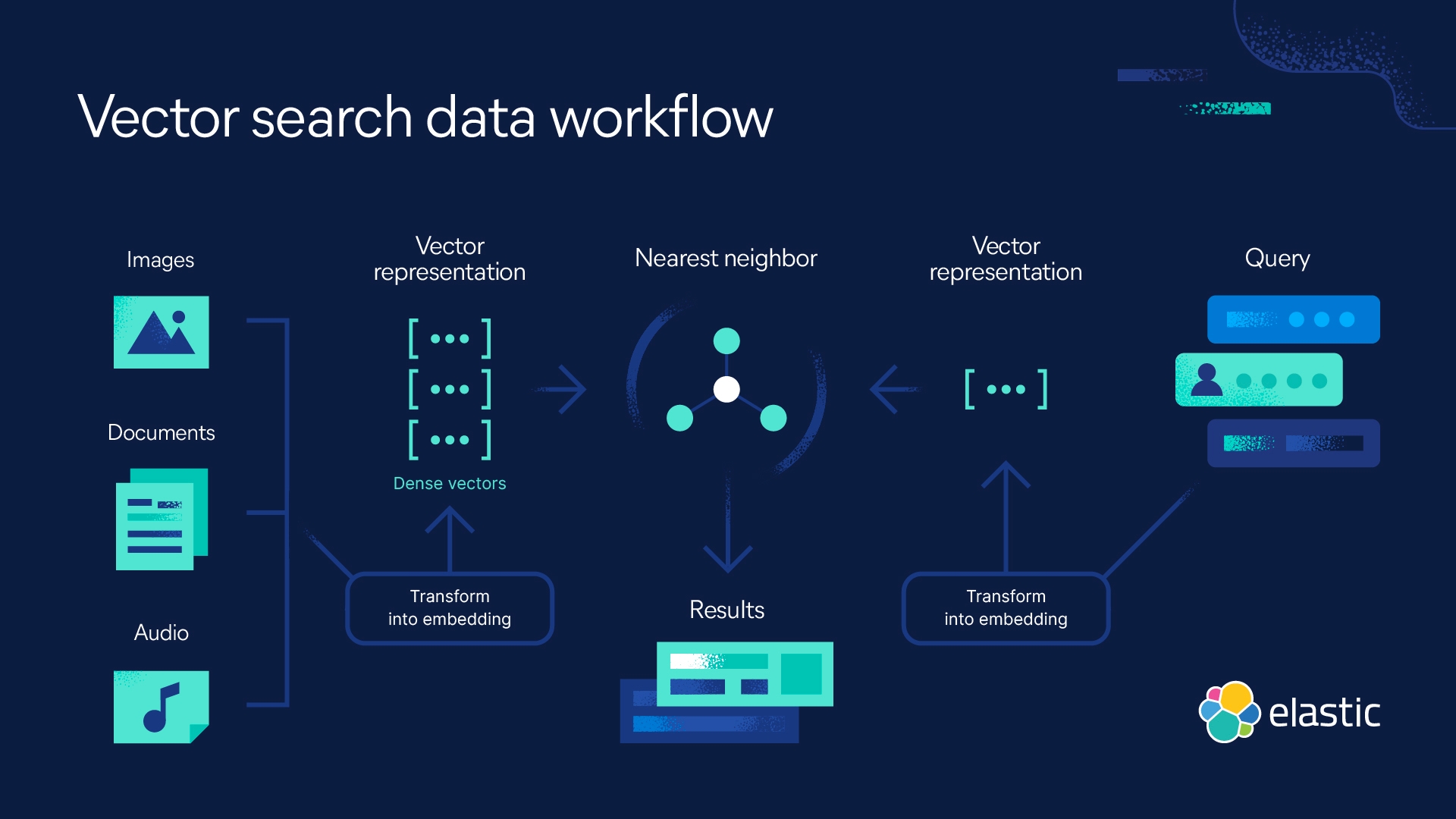
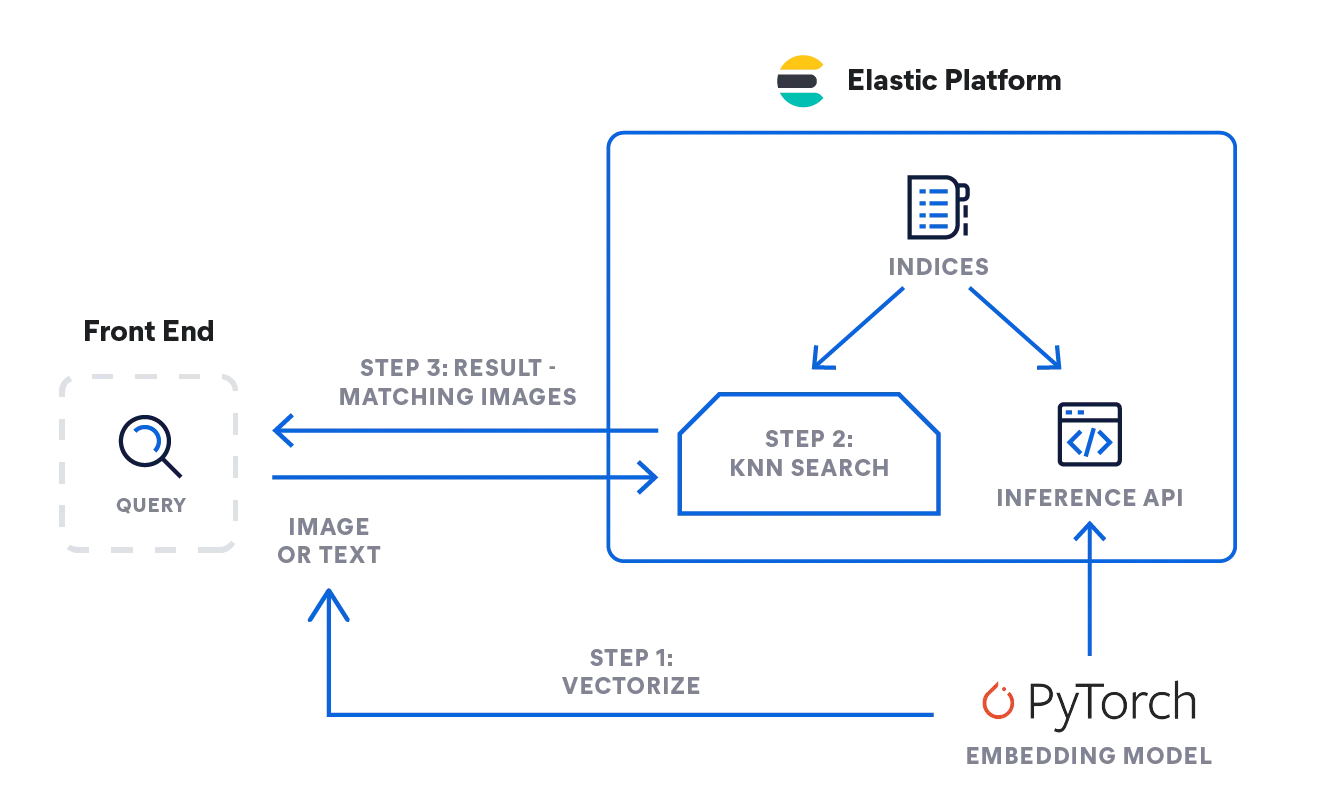
Elasticを使用したkNN検索
ElasticsearchがkNN検索の実装を支援します。Approximate kNNと正確なBrute-Force kNNという、2つの方法がサポートされます。類似性検索、NLPアルゴリズムに基づく関連性ランキング、製品の提案と推奨エンジンのコンテキストで、kNN検索を使用できます。
k近傍法に関するFAQ
k近傍法(kNN)とは?
kNNは、類似性に基づいて予測を行うために使用します。このような性質を持つkNNは、自然言語処理アルゴリズムのコンテキストにおける関連度ランキング、類似性検索と推奨エンジン、または製品の提案に使用できます。kNNは、データセットのサイズが比較的小さい場合に便利なこともポイントです。
kNNは教師ありと教師なし、どちらの機械学習ですか?
kNNは教師ありの機械学習です。一連のデータが与えられ、それを格納してクエリが実行されたときだけデータを処理します。
kNNの意味
kNNとはk近傍法アルゴリズムのことで、kは分析で考慮する最近傍の数を表します。
脚注
- Silverman, B.W.,& Jones, M.C.(1989)。E. フィックスおよびJLホッジ(1951):「An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation: Commentary on Fix and Hodges(ノンパラメトリック判別分析と密度推定への重要な貢献:フィックスとホッジに関する解説)」(1951)。国際統計協会(ISI)/ Revue Internationale de Statistique、57(3)、233–238。https://doi.org/10.2307/1403796
- T. カバーおよびP. ハート、「Nearest neighbor pattern classification(最近傍パターン分類)」『IEEE Transactions on Information Transactions on Information Transactions on Information』、vol.13, no. 1, pp. 21-27, January 1967, doi: 10.1109/TIT.1967.1053964。https://ieeexplore.ieee.org/document/1053964/authors#authors
- 「K-Nearest Neighbors Algorithm: Classification and Regression Star(k近傍法アルゴリズム:分類と回帰の星」、History of Data Science、2023年10月23日にアクセス、https://www.historyofdatascience.com/k-nearest-neighbors-algorithm-classification-and-regression-star/