Que sont les k plus proches voisins ?
Définition des k plus proches voisins
Les k plus proches voisins sont un algorithme de Machine Learning utilisant la proximité pour comparer un point de données avec un ensemble d'informations qui a été utilisé pour son entraînement et qu'il a mémorisé pour formuler des prédictions. Cet apprentissage fondé sur des instances a amené les k plus proches voisins à être qualifiés d'apprentissage « paresseux ». Ils permettent toutefois à l'algorithme de résoudre des problèmes de régression ou de classification. Les k plus proches voisins se débarrassent de la supposition que des points similaires peuvent se trouver à proximité les uns des autres selon le principe de « Qui se ressemble s'assemble ».
En leur qualité d'algorithme de classification, les k plus proches voisins attribuent un nouveau point de données à l'ensemble majoritaire qui se trouve à proximité. En tant qu'algorithme de régression, les k plus proches voisins formulent une prédiction en fonction de la moyenne des valeurs qui sont au plus près du point de la requête.
Les k plus proches voisins sont un algorithme de Machine Learning supervisé dans lequel les k représentent le nombre de plus proches voisins qui sont pris en compte dans la gestion du problème de régression ou de classification et où les plus proches voisins se situent le plus à proximité du nombre choisi pour les k.
Petite histoire de l'algorithme des k plus proches voisins
Les k plus proches voisins ont été développés pour la première fois par Evelyn Fix et Joseph Hodges en 1951 dans le contexte de la recherche effectuée par les forces armées américaines1. Ils ont publié un article présentant une analyse discriminante, qui est une méthode de classification non paramétrique. En 1967, Thomas Cover et Peter Hart ont élargi cette méthode et publié leur article intitulé "Nearest Neighbor Pattern Classification" (Classification des schémas des plus proches voisins2. Près de 20 ans plus tard, l'algorithme a été affiné par James Keller, qui a développé des "k plus proches voisins approximatifs" produisant des taux d'erreur inférieurs3.
Aujourd'hui, l'algorithme des k plus proches voisins est le plus largement utilisé grâce à son adaptabilité à la plupart des champs, depuis la génétique jusqu'à la finance et au service client.
Comment fonctionnent les k plus proches voisins ?
L'algorithme des k plus proches voisins fonctionne comme un algorithme d'apprentissage supervisé, il traite des ensembles de données d'entraînement qu'il mémorise. Il se fonde sur ces données d'entrée étiquetées pour apprendre une fonction qui génère une sortie appropriée lors de l'ingestion de nouvelles données non étiquetées.
Ainsi, l'algorithme est en mesure de résoudre des problèmes de régression ou de classification. Même si le calcul des k plus proches voisins survient dans le cadre d'une requête et pas lors de l'entraînement, il s'accompagne d'exigences importantes en matière de stockage des données. Par conséquent, il est fortement dépendant de la mémoire disponible.
Pour les problèmes de classification, l'algorithme des k plus proches voisins attribue une étiquette de classe en fonction d'une majorité définie. Ainsi, il utilise l'étiquette la plus souvent présente dans le voisinage d'un point de données précis. En d'autres termes, la sortie d'un problème de classification est le mode des voisins les plus proches.
Différence entre le vote majoritaire et le vote à majorité relative
Le vote majoritaire désigne les décisions prises à plus de 50 % de la majorité. Il s'applique lorsque deux étiquettes de classe sont retenues. En revanche, le vote à majorité relative s'applique si plusieurs étiquettes de classe sont prises en compte. Dans ce cas, un pourcentage de 33,30 % est suffisant pour constituer une majorité et ainsi formuler une prédiction. Par conséquent, le vote à majorité relative est l'expression la plus juste pour définir le mode des k plus proches voisins.
Nous pourrions illustrer la différence entre ces deux votes de la manière suivante :
Une prédiction binaire
Y : 🎉 🎉 🎉 ❤️❤️❤️❤️❤️
Vote majoritaire : ❤️
Vote à majorité relative : ❤️
Un contexte à plusieurs classes
Y : ⏰⏰⏰💰💰💰🏠🏠🏠🏠
Vote majoritaire : Aucun
Vote à majorité relative : 🏠
Les problèmes de régression utilisent la moyenne des voisins les plus proches pour prédire une classification. Un problème de régression génère une sortie de requête composée de vrais nombres.
Imaginons que vous créez un graphique afin de prédire le poids d'une personne en fonction de sa taille. Les valeurs indiquant la taille seraient indépendantes tandis que celles du poids seraient dépendantes. En calculant le rapport moyen entre le poids et la taille, vous pourriez estimer le poids d'une personne (soit la variable dépendante) en fonction de sa taille (c'est-à-dire la variable indépendante).
Les 4 types de calcul des indicateurs de distance des k plus proches voisins
La tâche principale de l'algorithme des k plus proches voisins consiste à déterminer la distance entre le point de la requête et les autres points de données. Le calcul d'un tel indicateur permet d'appliquer des limites aux décisions. qui créent plusieurs régions pour les points de données. Différentes méthodes permettent de calculer la distance :
- La distance euclidienne est la méthode la plus courante qui établit une ligne droite entre le point de la requête et les autres points mesurés.
- La distance de Manhattan est également une méthode populaire qui mesure la valeur absolue entre deux points. Elle est représentée sur une grille, souvent appelée taxi-distance, qui montre comment il est possible de se déplacer d'un point A (le point de votre requête) à un point B (le point mesuré).
- La distance de Minkowski est une généralisation des indicateurs de distance euclidienne et de Manhattan qui peut créer d'autres indicateurs de distance. Elle se calcule dans un espace vectoriel normé. Dans la distance de Minkowski, p est le paramètre qui définit le type de distance utilisé dans le calcul. Si p = 1, la distance de Manhattan est utilisée. Si p = 2, la distance euclidienne est utilisée.
- La distance de Hamming, également appelée indicateur de chevauchement, est une technique utilisée avec des vecteurs de chaîne ou booléens afin d'identifier les emplacements où les vecteurs ne sont pas en correspondance. En d'autres termes, elle mesure la distance entre deux chaînes de longueur égale. Elle est particulièrement utile pour détecter les erreurs et les codes de correction connexes.
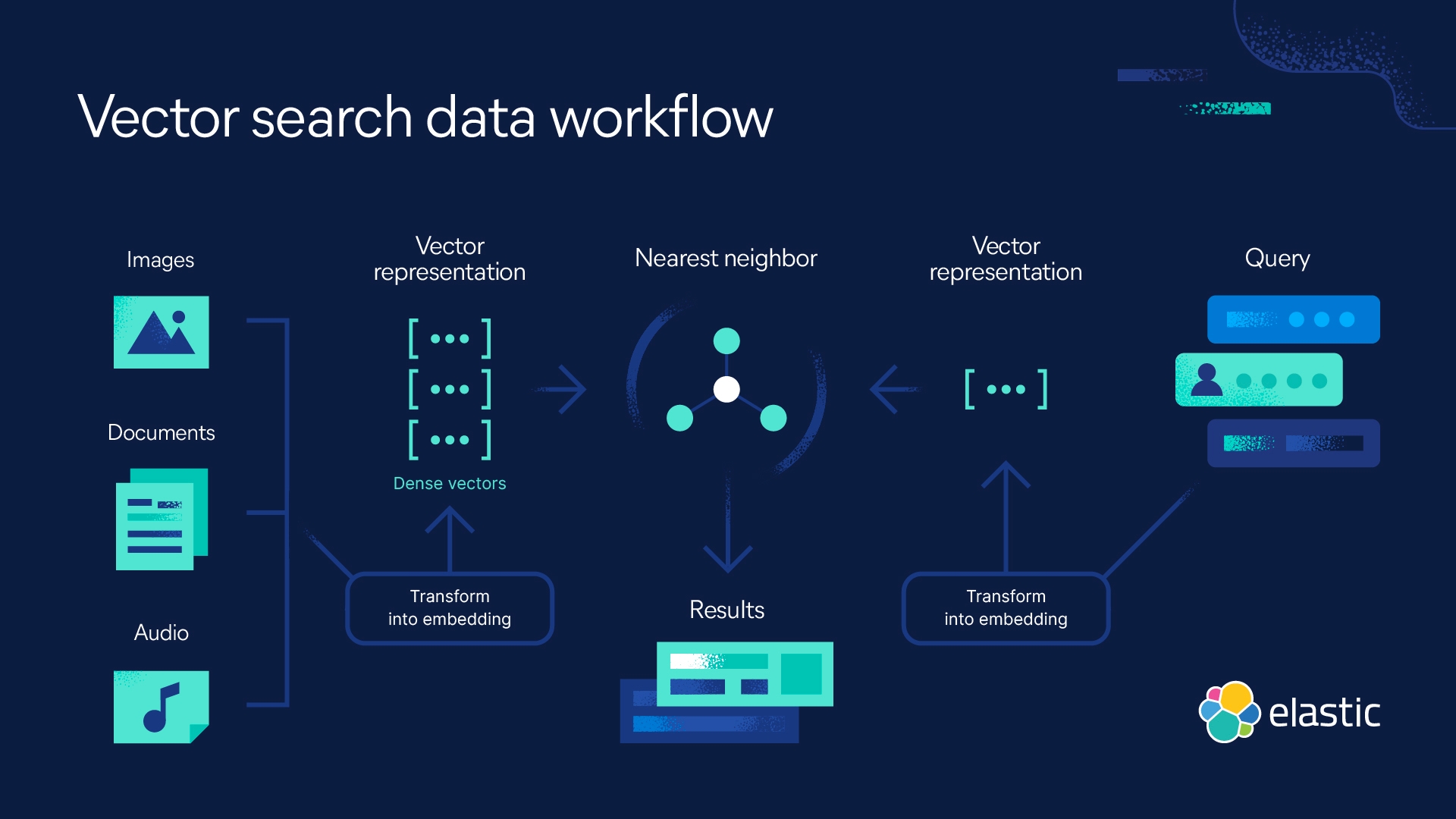
Comment choisir la meilleure valeur des k
Pour choisir la meilleure valeur des k (c'est-à-dire le nombre des plus proches voisins pris en compte), vous devez effectuer des expérimentations à l'aide de quelques valeurs afin de trouver celle des k générant les prédictions les plus précises à l'aide du plus petit nombre d'erreurs. La détermination de la meilleure valeur est une question d'équilibre :
- Les valeurs de k faibles rendent les prédictions instables.Imaginons un point de requête entouré de deux points verts et d'un triangle rouge. Si k = 1 et si le point le plus proche du point de la requête est l'un des points verts, l'algorithme prédira de manière erronée un point vert comme résultat de la requête. Les valeurs des k faibles comprennent des variances élevées (le modèle correspond de trop près aux données d'entraînement), des complexités élevées et des biais faibles (le modèle est suffisamment complexe pour bien correspondre aux données d'entraînement).
- Les valeurs des k élevées sont bruyantes.
Une valeur des k plus élevée augmente l'exactitude des prédictions, car la quantité de nombres permettant de calculer les modes ou les moyennes est plus importante. Toutefois, si la valeur des k est trop élevée, elle engendrera probablement une variance faible, une complexité faible et des biais élevés (le modèle n'est pas suffisamment complexe pour bien correspondre aux données d'entraînement).
Dans l'idéal, la valeur des k doit se situer entre une variance élevée et des biais élevés. En outre, il est recommandé de choisir un nombre impair pour les k afin d'éviter tout résultat nul lors de l'analyse de la classification.
La valeur des k appropriée dépend aussi de votre ensemble de données. Pour choisir cette valeur, vous devriez essayer de trouver la racine carrée de N, qui est le nombre de points de données dans l'ensemble d'entraînement. Les techniques de contre-validation peuvent également vous aider à choisir la valeur des k la mieux adaptée à votre ensemble de données.
Avantages de l'algorithme des k plus proches voisins
L'algorithme des k plus proches voisins est souvent décrit comme l'algorithme d'apprentissage supervisé "le plus simple", qui permet de bénéficier de plusieurs avantages :
- Simplicité : les k plus proches voisins sont faciles à mettre en œuvre grâce à leur fonctionnement simple et à leur précision. Ainsi, ils sont souvent l'un des premiers systèmes de classification que les data scientists apprennent à utiliser.
- Adaptable : lorsque de nouveaux échantillons d'entraînement sont ajoutés à son ensemble de données, l'algorithme des k plus proches voisins adapte ses prédictions afin de les inclure.
- Facilité de programmation : les k plus proches voisins nécessitent seulement quelques hyperparamètres (à savoir une valeur des k et un indicateur de distance). Ainsi, l'algorithme est relativement peu complexe.
En outre, l'algorithme des k plus proches voisins ne nécessite aucun temps d'entraînement, car il stocke les données d'entraînement et sa puissance de calcul est utilisée seulement pour la formulation de prédictions.
Défis et limitations des k plus proches voisins
Même si l'algorithme des k plus proches voisins est simple, il s'accompagne de plusieurs défis et limitations, notamment à cause de sa simplicité :
- Difficile à scaler : étant donné que les k plus proches voisins prennent beaucoup de mémoire et de stockage de données, les dépenses relatives au stockage augmentent. À cause de sa dépendance à la mémoire, l'algorithme est gourmand en capacité de calcul, qui requiert beaucoup de ressources.
- Malédiction de la dimensionnalité : cette expression désigne un phénomène survenant en science informatique, dans le cadre duquel un ensemble fixe d'exemples d'entraînement est remis en question par un nombre croissant de dimensions et l'augmentation inhérente des valeurs des fonctionnalités qu'elles contiennent. En d'autres termes, les données d'entraînement du modèle ne peuvent pas suivre le rythme de l'évolution de la dimension de l'hyperespace. Ainsi, les prédictions sont moins précises, car la distance entre le point de la requête et des points similaires s'agrandit dans d'autres dimensions.
- Sur-apprentissage : comme démontré précédemment, la valeur des k influe sur le comportement de l'algorithme. Cela peut arriver, en particulier quand la valeur des k est trop faible. Les valeurs des k plus faibles peuvent surapprendre les données, tandis que les valeurs de k plus élevées "lisseront" les valeurs de prédiction, car l'algorithme établit la moyenne des valeurs dans un domaine plus vaste.
Principaux cas d'utilisation des k plus proches voisins
Populaire grâce à sa simplicité et à sa précision, l'algorithme des k plus proches voisins a une variété d'applications, notamment quand il est utilisé pour l'analyse de la classification.
- Classement selon la pertinence : les k plus proches voisins utilisent des algorithmes de traitement du langage naturel afin d'identifier les résultats les plus pertinents pour une requête.
- Recherche par similarité d'images ou de vidéos : la recherche de similarités dans les images utilise des descriptions en langage naturel pour trouver des images correspondant à des requêtes textuelles.
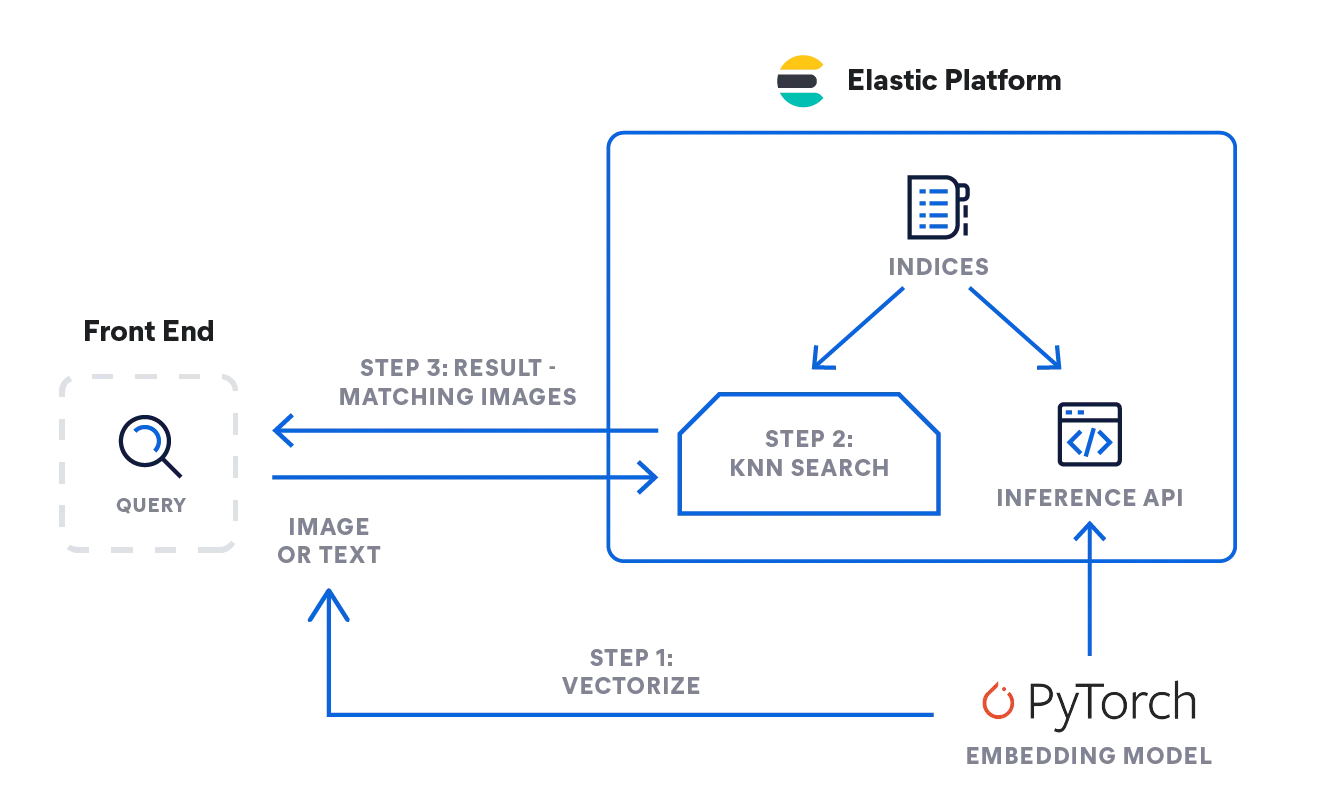
- Reconnaissance de schémas : les k plus proches voisins peuvent être utilisés pour identifier les tendances dans la classification textuelle ou numérique.
- Finance : dans le secteur financier, les k plus proches voisins peuvent être utilisés pour les prévisions financières et les taux de change de devise, entre autres.
- Recommandations de produits et moteurs de recommandation : Pensez à Netflix ! Quand, après avoir regardé un film ou une série, la plateforme vous en suggère d'autres. Tout site qui intègre ce type de fonction, ouvertement ou non, est susceptible d'utiliser un algorithme des k plus proches voisins pour propulser son moteur de recommandation.
- Santé : dans les domaines de la médecine et de la recherche médicale, l'algorithme des k plus proches voisins peut être utilisé en génétique pour calculer la probabilité de certaines expressions des gènes. Ainsi, les médecins peuvent définir le risque de cancer, de crise cardiaque et d'autres maladies héréditaires.
- Prétraitement des données : l'algorithme des k plus proches voisins peut être utilisé pour estimer les valeurs manquantes dans les ensembles de données.
Recherche des k plus proches voisins avec Elastic
Elasticsearch vous permet de mettre en œuvre la recherche des k plus proches voisins. Deux méthodes sont prises en charge, à savoir les k plus proches voisins approximatifs, d'une part, et les k plus proches voisins exacts et par force brute, d'autre part. Vous pouvez utiliser la recherche des k plus proches voisins dans le cadre de la recherche de similarités, du classement selon la pertinence en fonction des algorithmes de traitement du langage naturel, mais aussi des recommandations de produits et des moteurs de recommandation.
Mettez en œuvre la recherche des k plus proches voisins avec Elastic
FAQ sur les k plus proches voisins
Quand faut-il utiliser les k plus proches voisins ?
Utilisez les k plus proches voisins pour formuler des prédictions fondées sur la similarité. Vous pouvez recourir à la recherche des k plus proches pour le classement par pertinence dans le contexte des algorithmes de traitement du langage naturel, pour la recherche de similarités et les moteurs de recommandation ou pour les recommandations de produits. Il convient de noter que les k plus proches voisins sont utiles lorsque vous disposez d'un ensemble de données relativement petit.
Les k plus proches voisins sont-ils du Machine Learning supervisé ou non supervisé ?
Les k plus proches voisins sont du Machine Learning supervisé. L'algorithme utilise un ensemble de données qu'il stocke et en traite les informations uniquement dans le cadre d'une requête.
Que signifient les k plus proches voisins ?
Dans l'algorithme des k plus proches voisins, les k représentent le nombre des voisins les plus proches qui sont retenus pour l'analyse.
Notes
- Silverman, B.W., et Jones, M.C. (1989). E. Fix et J.L Hodes (1951) : Une contribution importante à l'analyse discriminante non paramétrique et à l'estimation de la densité : commentaire sur Fix et Hodges (1951). Institut international de statistique (ISI) / Revue Internationale de Statistique,57(3), 233-238. https://doi.org/10.2307/1403796
- T. Cover et P. Hart, "Nearest neighbor pattern classification", {i>IEEE Transactions on Information Theory<i}, vol. 13, n° 1, pp. 21-27, janvier 1967, doi : 10.1109/TIT.1967.1053964. https://ieeexplore.ieee.org/document/1053964/authors#authors
- Algorithme des K plus proches voisins : étoile de classification et de régression, histoire de la science des données, consulté le 23/10/2023, https://www.historyofdatascience.com/k-nearest-neighbors-algorithm-classification-and-regression-star/