kNN이란 무엇인가요?
K-최근접 이웃 정의
kNN(K-최근접 이웃 알고리즘)은 학습한 후 저장된 데이터 세트와 하나의 데이터 요소를 근접성을 이용해 비교하고 예측을 수행하는 머신 러닝 알고리즘입니다. 이러한 인스턴스 기반 학습으로 kNN에는 '게으른 학습'이라는 명칭이 붙었으며, 이는 알고리즘이 분류 또는 회귀 문제를 처리할 수 있도록 합니다. kNN은 유사한 요소가 서로 가까이에 위치한다는 가정에 기반합니다. 즉, "끼리끼리 모인다"는 속담과 같습니다.
분류 알고리즘으로서 kNN은 이웃한 데이터 중 다수 세트에 새로운 데이터 요소를 할당합니다. 회귀 알고리즘인 kNN은 쿼리 지점에 가장 가까운 값의 평균을 기반으로 예측을 수행합니다.
kNN은 지도 학습 알고리즘으로, 여기서 'k'는 분류 또는 회귀 문제에서 고려되는 최근접 이웃의 수를 나타내고, 'NN'은 k로 선택된 수에 대한 최근접 이웃을 나타냅니다.
kNN 알고리즘의 간략한 역사
kNN은 미군을 위해 수행된 연구 중 1951년 Evelyn Fix와 Joseph Hodges가 처음 개발했습니다1. 그들은 비모수적 분류 방법인 판별 분석을 설명하는 논문을 발표했습니다. 1967년에 Thomas Cover와 Peter Hart는 비모수적 분류 방법을 확장하여 "Nearest Neighbor Pattern Classification" 논문2을 발표했습니다. 거의 20년이 지난 후, James Keller는 더 낮은 오류율을 생성하는 "퍼지 KNN"을 개발하여 이 알고리즘을 개선하였습니다3.
오늘날 kNN 알고리즘은 유전학부터 금융, 고객 서비스에 이르기까지 대부분의 분야에 적용할 수 있어 가장 널리 사용되는 알고리즘입니다.
kNN은 어떻게 작동하나요?
kNN 알고리즘은 지도 학습 알고리즘으로서 작동합니다. 즉, 기억하는 훈련 데이터 세트를 제공받습니다. 레이블이 지정되지 않은 새로운 데이터가 주어졌을 때 적절한 출력을 생성하는 함수를 학습하기 위해 레이블이 지정된 해당 입력 데이터에 의존합니다.
이를 통해 알고리즘은 분류 또는 회귀 문제를 해결할 수 있습니다. kNN의 계산은 훈련 단계가 아닌 쿼리 중에 발생하지만 중요한 데이터 저장 요구 사항이 있으므로 메모리에 크게 의존합니다.
분류 문제의 경우 KNN 알고리즘은 다수를 기반으로 클래스 레이블을 할당합니다. 즉, 주어진 데이터 요소 주변에 가장 자주 나타나는 레이블을 사용합니다. 다시 말해, 분류 문제의 출력은 최근접 이웃들의 최빈값입니다.
구별: 다수결 투표와 복수 투표의 비교
다수결 투표에서는 50%가 넘으면 다수로 간주합니다. 이는 고려 중인 두 가지 클래스 레이블이 있는 경우에 적용됩니다. 그러나 여러 클래스 레이블을 고려하는 경우에는 복수 투표가 적용됩니다. 이러한 경우 33.3% 이상이면 다수를 나타내기에 충분하므로 예측이 가능합니다. 따라서 복수 투표는 kNN 최빈값을 정의하는 데 더 정확한 용어입니다.
이 차이점을 설명하자면 다음과 같습니다.
이진 예측
Y: 🎉🎉🎉❤️❤️❤️❤️❤️
다수결 투표: ❤️
복수 투표: ❤️
다중 클래스 설정
Y: ⏰⏰⏰💰💰💰🏠🏠🏠🏠
다수결 투표: 없음
다수결 투표: 🏠
회귀 문제는 가장 가까운 이웃들의 평균을 사용하여 분류를 예측합니다. 회귀 문제는 쿼리 출력으로 실수를 생성합니다.
예를 들어, 키를 기준으로 사람의 체중을 예측하는 차트를 만드는 경우 키를 나타내는 값은 독립적인 반면 체중 값은 종속적입니다. 평균 키-체중 비율을 계산하면 키(독립 변수)를 기준으로 사람의 체중(종속 변수)을 추정할 수 있습니다.
kNN 거리 메트릭을 계산하는 4가지 유형
kNN 알고리즘의 핵심은 쿼리 지점과 다른 데이터 지점 사이의 거리를 결정하는 것입니다. 거리 메트릭을 결정하면 결정 경계가 가능해집니다. 이러한 경계는 다양한 데이터 지점 영역을 만듭니다. 거리를 계산하는 데 사용되는 방법은 다양합니다.
- 유클리드 거리는 가장 일반적인 거리 측정법으로, 쿼리 지점과 다른 측정 대상 지점 사이의 직선 거리를 측정합니다.
- 맨해튼 거리도 널리 사용되는 측정법으로, 두 지점 사이의 절대값을 측정합니다. 그리드상에 표시되며 흔히 택시 기하학이라고도 하는데, A 지점(쿼리 지점)에서 B 지점(측정 대상 지점)까지 어떻게 이동하는지를 의미합니다.
- 민코프스키 거리는 유클리드 거리와 맨해튼 거리 메트릭을 일반화한 것으로, 다른 거리 메트릭을 생성할 수 있게 해줍니다. 이는 정규화된 벡터 공간에서 계산됩니다. 민코프스키 거리에서 p는 계산에 사용되는 거리 유형을 정의하는 매개변수입니다. p=1이면 맨해튼 거리가 사용됩니다. p=2이면 유클리드 거리가 사용됩니다.
- 해밍 거리는 중첩 메트릭이라고도 하며, 부울 또는 스트링 벡터에서 벡터가 일치하지 않는 위치를 식별하기 위해 사용되는 기술입니다. 즉, 길이가 같은 두 스트링 사이의 거리를 측정합니다. 특히 오류 탐지 및 오류 수정 코드에 유용합니다.
최적의 k 값을 선택하는 방법
최적의 k 값(고려된 최근접 이웃의 수)을 선택하려면 몇 가지 값을 실험하여 가장 적은 수의 오류로 가장 정확한 예측을 생성하는 k 값을 찾아야 합니다. 최적의 값을 결정하는 것은 균형을 맞추는 작업입니다.
- k 값이 낮으면 예측이 불안정해집니다.쿼리 지점이 녹색 점 2개와 빨간색 삼각형 1개로 둘러싸여 있다고 가정해 보겠습니다. k=1이고 쿼리 지점에 가장 가까운 지점이 녹색 점 중 하나인 경우 알고리즘은 녹색 점을 쿼리 결과로 잘못 예측합니다. k 값이 낮다는 것은 높은 분산(모델이 훈련 데이터에 너무 가깝게 적합함), 높은 복잡성, 낮은 편향(모델이 훈련 데이터에 잘 맞을 만큼 충분히 복잡함)을 의미합니다.
- k 값이 높으면 잡음이 끼게 됩니다.k 값이 높을수록 최빈값이나 평균을 계산할 수 있는 숫자가 많아지기 때문에 예측의 정확도가 높아집니다. 그러나 k 값이 너무 높으면 분산과 복잡도가 낮으며 편향이 높을 수 있습니다(모델이 훈련 데이터에 잘 맞을 만큼 복잡하지 않음).
이상적으로는 높은 분산과 높은 편향 사이의 균형을 이루는 k 값을 찾아야 합니다. 또한 분류 분석에서 동점을 피하기 위해 k 값을 홀수로 선택하는 것이 좋습니다.
적합한 k 값은 데이터 세트와도 관련이 있습니다. 해당 값을 선택하려면 N의 제곱근을 찾아야 합니다. 여기서 N은 훈련 데이터 세트의 데이터 요소 수입니다. 교차 검증 전략도 데이터 세트에 가장 적합한 k 값을 선택하는 데 도움이 될 수 있습니다.
kNN 알고리즘의 장점
kNN 알고리즘은 종종 "가장 간단한" 지도 학습 알고리즘으로 설명되며, 이는 다음과 같은 몇 가지 장점을 제공합니다.
- 간단함: kNN은 단순하고 정확하기 때문에 구현이 용이합니다. 따라서 이는 데이터 과학자가 배우는 첫 번째 분류기 중 하나로 종종 사용됩니다.
- 적응력: 새로운 훈련 샘플이 데이터 세트에 추가되면 kNN 알고리즘은 그 새로운 훈련 데이터를 포함하도록 예측을 즉시 조정합니다.
- 쉽게 프로그래밍 가능: kNN에는 k 값과 거리 메트릭 등 몇 가지 하이퍼파라미터만 필요합니다. 이는 알고리즘을 상당히 단순하게 만듭니다.
또한 kNN 알고리즘은 훈련 데이터를 저장하고 예측에만 계산 능력을 사용하므로 훈련 시간이 필요하지 않습니다.
kNN의 과제와 한계
kNN 알고리즘은 단순하지만, 그 단순성으로 인해 다음과 같은 몇 가지 과제와 한계를 지니고 있습니다.
- 확장하기 어려움: kNN은 많은 메모리와 데이터 저장 공간을 차지하므로 저장과 관련된 비용이 증가합니다. 메모리에 대한 이러한 의존성은 알고리즘이 계산 집약적이며, 결과적으로 리소스 소모가 크다는 것을 의미합니다.
- 차원의 저주: 이는 컴퓨터 과학에서 일어나는 현상을 가리키는 말로, 차원 수가 늘어나고 이러한 차원에 특징 값이 본질적으로 증가함에 따라 고정된 훈련 예제 세트가 어려움을 겪는 것을 말합니다. 다시 말해, 모델의 훈련 데이터는 진화하는 초공간의 차원을 따라잡을 수 없습니다. 즉, 쿼리 지점과 유사한 지점 사이의 거리가 다른 차원에서 더 멀어지기 때문에 예측의 정확도가 떨어집니다.
- 과적합: 앞에서 설명한 것처럼 k 값은 알고리즘의 동작에 영향을 미칩니다. 이는 특히 k 값이 너무 낮을 때 발생할 수 있습니다. k 값이 낮을수록 데이터를 과적합시킬 수 있는 반면, k 값이 높을수록 알고리즘은 더 넓은 영역에 대해 값의 평균을 계산하므로 예측 값이 '평활'해집니다.
주요 kNN 사용 사례
단순성과 정확성으로 널리 알려진 kNN 알고리즘은 특히 분류 분석에 사용될 때 다양한 용도로 사용됩니다.
- 관련성 순위: kNN은 자연어 처리(NLP) 알고리즘을 사용하여 쿼리와 가장 관련성이 높은 결과를 결정합니다.
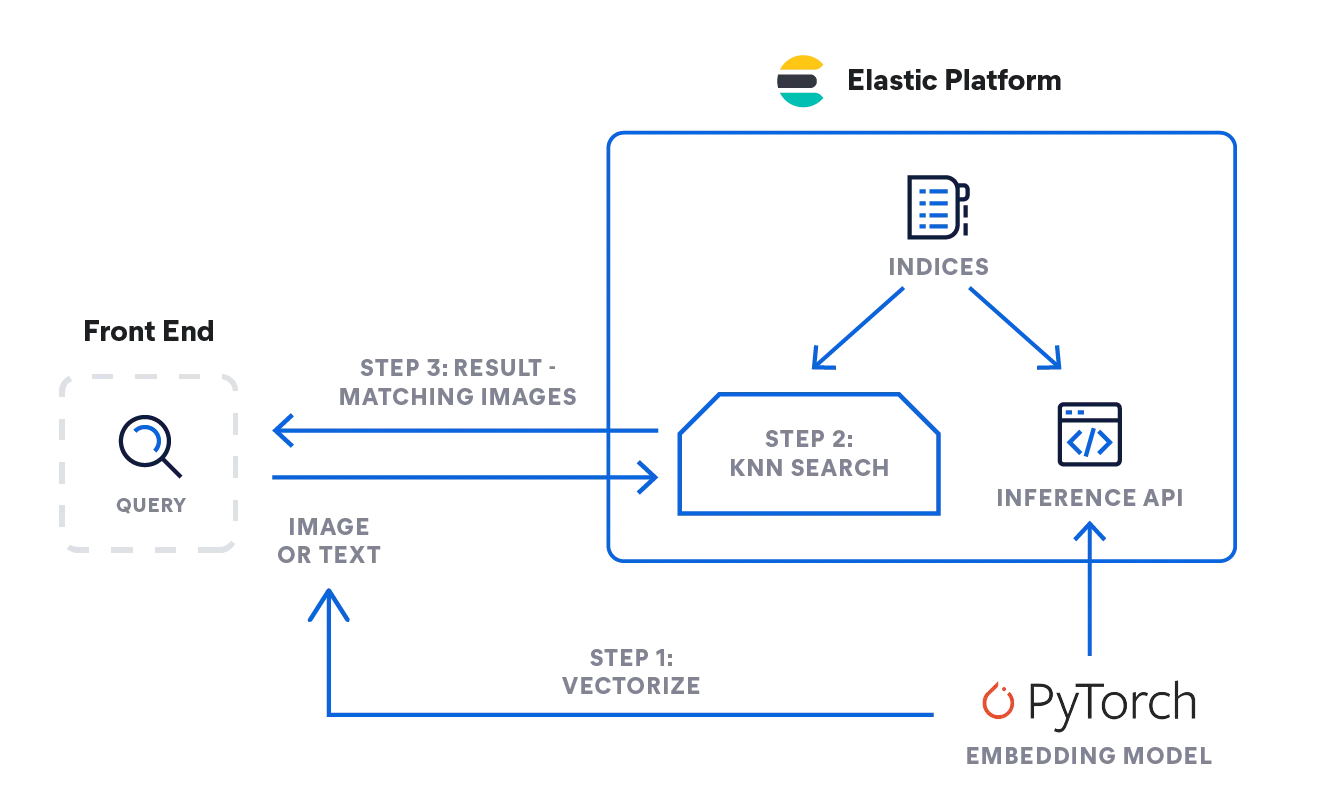
- 이미지 또는 동영상에 대한 유사성 검색: 이미지 유사성 검색은 자연어 설명을 사용하여 텍스트 쿼리와 일치하는 이미지를 찾습니다.
- 패턴 인식: kNN은 텍스트 또는 숫자 분류에서 패턴을 식별하는 데 사용할 수 있습니다.
- 금융: 금융 부문에서는 kNN을 주식 시장 예측, 환율 등에 사용할 수 있습니다.
- 제품 추천 및 추천 엔진: 넷플릭스를 생각해보세요! "이 콘텐츠가 마음에 드셨다면, 이것도 마음에 드실 거예요." 같은 문장을 명시적으로든 암묵적으로든 사용하는 사이트라면 추천 엔진을 구동하기 위해 kNN 알고리즘을 사용하고 있을 가능성이 높습니다.
- 의료: 의학 및 의료 연구 분야에서 kNN 알고리즘은 유전학에서 특정 유전자 발현 확률을 계산하는 데 사용될 수 있습니다. 이를 통해 의사는 암, 심장마비 또는 기타 유전 질환의 가능성을 예측할 수 있습니다.
- 데이터 전처리: kNN 알고리즘은 데이터 세트에서 누락된 값을 추정하는 데 사용할 수 있습니다.
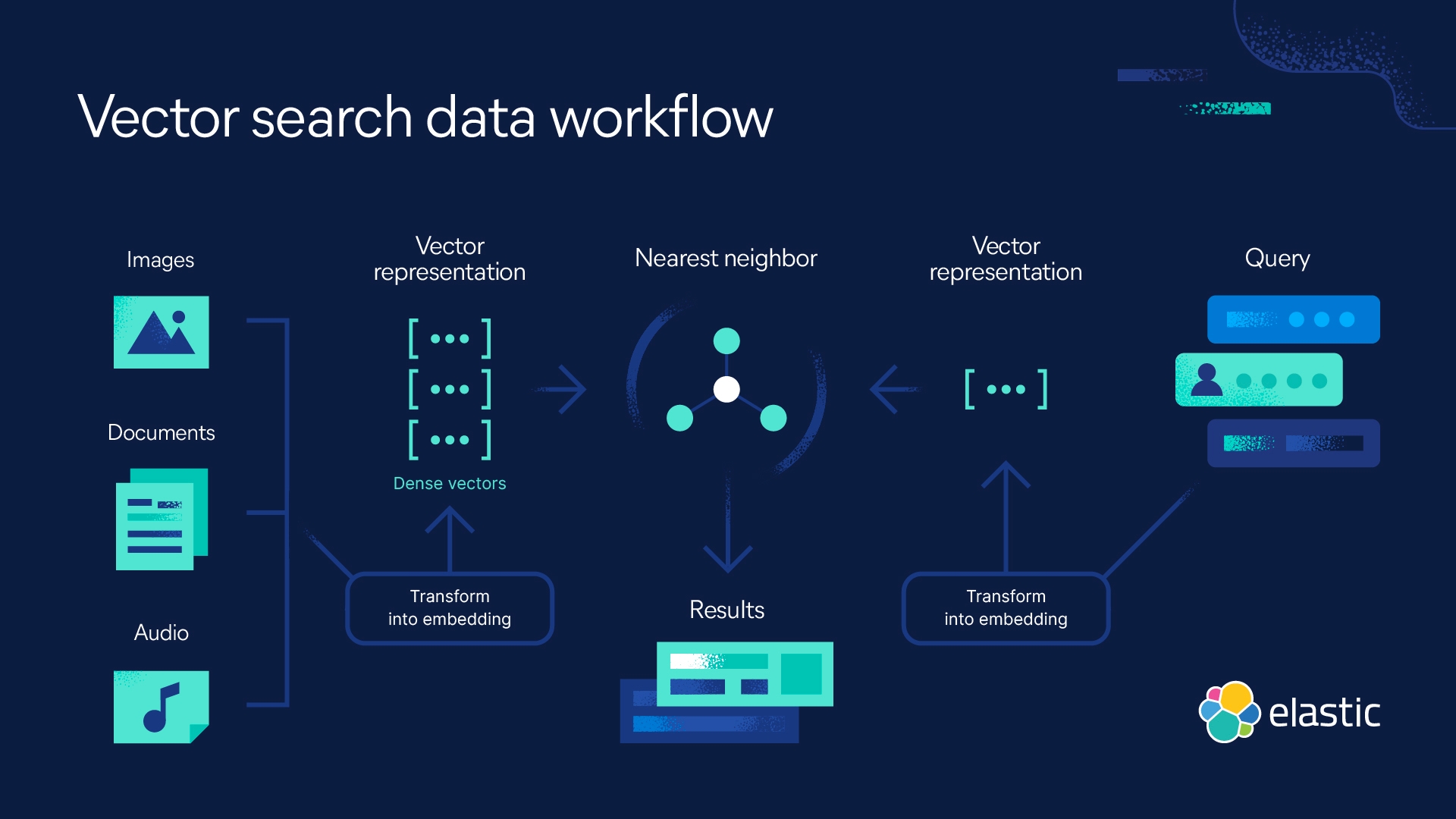
Elastic을 사용한 kNN 검색
Elasticsearch를 사용하면 kNN 검색을 구현할 수 있습니다. 근사 kNN과 정확한 무차별 kNN의 두 가지 방법이 지원됩니다. 유사성 검색, NLP 알고리즘을 기반으로 한 정확도 순위, 제품 추천 및 추천 엔진의 맥락에서 kNN 검색을 사용할 수 있습니다.
K-최근접 이웃 FAQ
kNN은 언제 사용하나요?
kNN은 유사성을 기반으로 예측할 때 사용합니다. 따라서 자연어 처리 알고리즘 맥락에서 유사성 검색 및 추천 엔진, 또는 제품 추천에 정확도 순위를 매기는 데 kNN을 사용할 수 있습니다. kNN은 상대적으로 작은 데이터 세트가 있을 때 유용합니다.
kNN은 지도 머신 러닝인가요, 비지도 머신 러닝인가요?
kNN은 지도 머신 러닝입니다. 이는 데이터를 입력받아 저장하고, 쿼리될 때만 데이터를 처리합니다.
kNN은 무엇의 약자인가요?
kNN은 k-최근접 이웃 알고리즘의 약자이며, 여기서 k는 분석에서 고려되는 최근접 이웃의 수를 나타냅니다.
각주
- Silverman, B.W., & Jones, M.C.(1989). E. Fix 및 J.L Hodes(1951): An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation: Commentary on Fix and Hodges(1951). 국제통계기구(ISI) / Revue Internationale de Statistique,57(3), 233–238. https://doi.org/10.2307/1403796
- T. Cover 및 P. Hart, "Nearest neighbor pattern classification," IEEE Transactions on Information Theory에 게재, vol. 13, no. 1, pp. 21-27, 1967년 1월, doi: 10.1109/TIT.1967.1053964. https://ieeexplore.ieee.org/document/1053964/authors#authors
- K-Nearest Neighbors Algorithm: Classification and Regression Star, History of Data Science, 열람일: 2023/10/23, https://www.historyofdatascience.com/k-nearest-neighbors-algorithm-classification-and-regression-star/