Was bedeutet kNN?
Definition: K-Nearest-Neighbor
Der kNN- oder auch K-Nearest-Neighbor-Algorithmus ist ein nähebasierter Machine-Learning-Algorithmus, der Datenpunkte mit dem Datensatz vergleicht, mit dem er trainiert wurde und den er für Vorhersagen gespeichert hat. Dieses instanzenbasierte Lernen verleiht kNN die Bezeichnung „Lazy Learning“ („träges Lernen“) und ermöglicht dem Algorithmus, Klassifizierungs- oder Regressionsprobleme durchzuführen. kNN geht von der Annahme aus, dass ähnliche Punkte in der Nähe voneinander gefunden werden können – Gleich und Gleich gesellt sich gern.
Als Klassifizierungsalgorithmus weist kNN neue Datenpunkte der Mehrheitsmenge innerhalb ihrer Nachbarn zu. Als Regressionsalgorithmus trifft kNN Vorhersagen anhand des Durschnitts der Werte in der Nähe des Abfragepunkts.
kNN ist ein beaufsichtigter Lernalgorithmus, bei dem „k“ für die Anzahl der nächsten Nachbarn steht, die für das Klassifizierungs- bzw. Regressionsproblem berücksichtigt werden, während „NN“ für die nächsten Nachbarn der für „k“ ausgewählten Zahl steht.
Eine kurze Geschichte des k-Nearest-Neighbor-Algorithmus
kNN wurde ursprünglich im Jahr 1951 von Evelyn Fix und Joseph Hodges bei ihrer Forschungsarbeit für das US-Militär entwickelt1. Sie veröffentlichten eine Erklärung zur Trennschärfeanalyse, einer nichtparametrischen Klassifizierungsmethode. 1967 erweiterten Thomas Cover und Peter Hart diese nichtparametrische Klassifizierungsmethode und veröffentlichten ihren Artikel „Nearest Neighbor Pattern Classification“2. Beinahe 20 Jahre später wurde der Algorithmus von James Keller als „Fuzzy kNN“ weiterentwickelt, um die Fehlerraten zu reduzieren3.
Heutzutage ist der kNN-Algorithmus aufgrund seiner Anpassbarkeit an verschiedenste Bereiche – von Genetik über Finanzen bis hin zum Kundenservice – sehr weit verbreitet.
Wie funktioniert kNN?
Der kNN-Algorithmus ist ein beaufsichtigter Lernalgorithmus, d. h. er wird mit Trainingsdaten gefüttert und merkt sich diese Daten. Anhand dieser unbeschrifteten Daten lernt der Algorithmus eine Funktion, die für neue, unbeschriftete Daten eine passende Ausgabe liefert.
Auf diese Weise kann der Algorithmus Klassifizierungs- oder Regressionsprobleme lösen. Die Berechnung von kNN erfolgt zwar zur Abfragezeit und nicht während der Trainingsphase, aber der Algorithmus hat wichtige Datenspeicheranforderungen und ist daher recht arbeitsspeicherintensiv.
Für Klassifizierungsprobleme weist der kNN-Algorithmus eine mehrheitsbasierte Klassenbeschriftung zu und verwendet also die Beschriftung, die um einen bestimmten Datenpunkt herum am häufigsten auftritt. Die Ausgabe eine Klassifizierungsproblems ist also der Modus der nächsten Nachbarn.
Wichtige Unterscheidung: Mehrheitsbeschluss und Pluralitätsbeschluss
Beim Mehrheitsbeschluss gilt jeder Wert über 50 % als Mehrheit. Dies gilt auch, wenn zwei Klassenbeschriftungen betrachtet werden. Wenn wir jedoch mehrere Klassenbeschriftungen betrachten, kommt der Pluralitätsbeschluss zum Einsatz. In diesen Fällen reichen 33,3 % aus, um eine Mehrheit zu bilden und eine Vorhersage zu treffen. Der Pluralitätsbeschluss ist daher die passende Beschreibung für den kNN-Modus.
Sehen wir uns eine Abbildung dieser Unterscheidung an:
Eine binäre Vorhersage
Y: 🎉🎉 🎉 ❤️❤️❤️❤️❤️
Mehrheitsbeschluss: ❤️
Pluralitätsbeschluss: ❤️
Situation mit mehreren Klassen
Y: ⏰⏰⏰ 💰 💰 💰 🏠 🏠 🏠 🏠
Mehrheitsbeschluss: Keine
Pluralitätsbeschluss: 🏠
Regressionsprobleme verwenden den Mittelwert der nächsten Nachbarn, um eine Klassifizierung vorherzusagen. Regressionsprobleme liefern Zahlenwerte als Ausgabe von Abfragen.
Angenommen, Sie erstellen ein Diagramm, um das Gewicht von Personen anhand ihrer Größe vorherzusagen, dann sind die Werte für die Größe unabhängig und die Werte für das Gewicht abhängig. Anhand des durchschnittlichen Verhältnisses zwischen Körpergröße und Gewicht können Sie das Gewicht einer Person (abhängige Variable) anhand von deren Größe (unabhängige Variable) schätzen.
Vier Berechnungsarten für kNN-Distanzmetriken
Der Schlüssel zum kNN-Algorithmus ist die Ermittlung der Distanz zwischen dem Abfragepunkt und den anderen Datenpunkten. Anhand von Distanzmetriken können wir Entscheidungsgrenzen aufstellen. Diese Grenzen bilden unterschiedliche Datenpunktregionen. Es gibt verschiedene Methoden für die Distanzberechnung:
- Die Euklidische Distanz ist die am häufigsten verwendete Distanzmessung und verwendet eine gerade Linie zwischen dem Abfragepunkt und dem anderen gemessenen Punkt.
- Die Manhattan-Distanz ist ebenfalls eine beliebte Distanzmessung, die den absoluten Wert zwischen zwei Punkten ermittelt. Sie wird auf einem Raster dargestellt und manchmal auch als „Taxi“-Geometrie bezeichnet: Wie gelangt man von Punkt A (dem Abfragepunkt) nach Punkt B (dem gemessenen Punkt)?
- Die Minkowski-Distanz ist eine Verallgemeinerung der Euklidischen und der Manhattan-Distanzmetriken und ermöglicht die Schaffung neuer Distanzmetriken. Sie wird in einem genormten Vektorraum berechnet. Bei der Minkowski-Distanz ist „p“ der Parameter, der die bei der Berechnung zu verwendende Distanz definiert. Für p=1 wird die Manhattan-Distanz verwendet. Für p=2 wird die Euklidische Distanz verwendet.
- Die Hamming-Distanz wird manchmal auch als Überlappungsmetrik bezeichnet und verwendet boolesche oder Zeichenfolgenvektoren, um zu identifizieren, wo Vektoren nicht übereinstimmen. Sie misst also die Distanz zwischen zwei Zeichenfolgen mit gleicher Länge. Dies ist besonders hilfreich für die Fehlererkennung und für Fehlerkorrekturcodes.
Auswahl des optimalen Werts für „k“
Um den besten „k“-Wert – die Anzahl der berücksichtigten nächsten Nachbarn – auszuwählen, müssen Sie einige Werte ausprobieren, um herauszufinden, welche „k“-Werte die exaktesten Vorhersagen mit der geringsten Fehleranzahl liefern. Die Ermittlung des besten Werts ist ein Balanceakt:
- Niedrigere „k“-Werte führen zu instabilen Vorhersagen.
Zum Beispiel: Ein Abfragepunkt ist umgeben von zwei grünen Punkten und einem roten Dreieck. Wenn k=1 ist und der Punkt einem der grünen Punkte am nächsten liegt, dann gibt der Algorithmus fälschlicherweise einen grünen Punkt als Ergebnis der Abfrage zurück. Niedrige „k“-Werte bedeuten eine hohe Varianz (das Modell passt zu gut zu den Trainingsdaten), hohe Komplexität und niedrige Verzerrung (das Modell ist komplex genug, um gut zu den Trainingsdaten zu passen). - Hohe „k“-Werte führen zu mehr Rauschen.
Höhere „k“-Werte verbessern die Genauigkeit der Vorhersagen, da die Modi oder Mittelwerte anhand von mehr Zahlen berechnet werden. Zu hohe „k“-Werte führen jedoch oft zu niedriger Varianz, niedriger Komplexität und starker Verzerrung (das Modell ist NICHT komplex genug, um gut zu den Trainingsdaten zu passen).
Im Idealfall sollten Sie einen „k“-Wert verwenden, der einen Mittelweg zwischen hoher Varianz und starker Verzerrung bildet. Außerdem ist es hilfreich, ungerade Werte für „k“ zu verwenden, um Gleichstände bei der Klassifizierungsanalyse zu vermeiden.
Der optimale „k“-Wert hängt auch von Ihrem Datensatz ab. Um den richtigen Wert zu finden, können Sie versuchen, die Quadratwurzel von „N“ zu ermitteln, wobei „N“ die Anzahl der Datenpunkte im Trainingsdatensatz ist. Kreuzvalidierungstechniken sind oft auch hilfreich, um den passenden „k“-Wert für Ihren Datensatz auszuwählen.
Vorteile des kNN-Algorithmus
Der kNN-Algorithmus wird oft als der einfachste beaufsichtigte Lernalgorithmus bezeichnet, wodurch sich mehrere Vorteile ergeben:
- Einfachheit: kNN ist aufgrund der Einfachheit und Genauigkeit auch recht einfach zu implementieren. Daher ist dies oft eine der ersten Klassifizierungsmethoden, die Datenwissenschaftler kennenlernen.
- Anpassbar: Sobald neue Trainingsdaten zum Datensatz hinzugefügt werden, passt der kNN-Algorithmus die Vorhersagen unter Berücksichtigung dieser neuen Daten an.
- Einfach zu programmieren: kNN erfordert nur wenige Hyperparameter: einen „k“-Wert und eine Distanzmetrik. Damit ist dieser Algorithmus relativ unkompliziert.
Außerdem erfordert der kNN-Algorithmus keine Trainingszeit, da die Trainingsdaten zunächst nur gespeichert werden und die Rechenleistung erst zum Vorhersagezeitpunkt eingesetzt wird.
Herausforderungen und Einschränkungen des kNN-Algorithmus
Der kNN-Algorithmus ist zwar einfach, ist daher aber auch mit einigen Herausforderungen und Einschränkungen verbunden:
- Schwer zu skalieren: Der kNN-Algorithmus verbraucht viel Arbeits- und Datenspeicher und ist daher mit recht hohen Speicherkosten verbunden. Aufgrund der Arbeitsspeicherabhängigkeit ist dieser Algorithmus auch rechenintensiv, was sich wiederum auf andere Ressourcen auswirkt.
- Fluch der Dimensionalität: Dies ist ein Phänomen in der Informatik, bei dem ein fester Satz an Trainingsbeispielen durch eine Zunahme der Dimensionen und die dadurch entstehende Zunahme an Merkmalswerten in diesen Dimensionen unbrauchbar wird. Die Trainingsdaten des Modells können also mit der wachsenden Dimensionalität des Hyperraums nicht mithalten. Dadurch werden die Vorhersagen ungenauer, da die Distanz zwischen dem Abfragepunkt und ähnlichen Punkten zunimmt – in anderen Dimensionen.
- Überanpassung: Der Wert von k wirkt, wie bereits gezeigt, auf das Verhalten des Algorithmus. Dies ist besonders bei zu niedrigen „k“-Werten der Fall. Niedrigere „k“-Werte können zu einer Überanpassung führen, während höhere Werte die Vorhersagen „glätten“, da der Algorithmus die Werte über einen größeren Bereich mittelt.
Wichtigste Anwendungsfälle für den kNN-Algorithmus
Der für seine Einfachheit und Genauigkeit beliebte kNN-Algorithmus kommt in vielen Bereichen zum Einsatz, insbesondere für Klassifizierungsanalysen.
- Relevanzrangfolgen: kNN verwendet Algorithmen für natürliche Sprachverarbeitung (Natural Language Processing, NLP), um die relevantesten Ergebnisse für eine Abfrage zu ermitteln.
- Ähnlichkeitssuche für Bilder oder Videos: Die Bildähnlichkeitssuche verwendet Beschreibungen in natürlicher Sprache, um passende Bilder anhand von Textabfragen zu finden.
- Mustererkennung: kNN kann eingesetzt werden, um Muster in Text- oder Zahlenklassifizierungen zu finden.
- Finanzen: kNN wird im Finanzwesen eingesetzt, um Vorhersagen für Aktienmärkte, Wechselkurse usw. zu treffen.
- Produktempfehlungen und Empfehlungsmaschinen: Denken Sie an Netflix! À la „Wenn Ihnen das gefallen hat, wird Ihnen das sicher auch gefallen...“ Jede Website, die eine Version dieses Satzes verwendet, ob offenkundig oder nicht, nutzt wahrscheinlich einen kNN-Algorithmus, um die Empfehlungsmaschine zu betreiben.
- Gesundheitswesen: In der Medizin und der medizinischen Forschung wird der kNN-Algorithmus eingesetzt, um die Wahrscheinlichkeit bestimmter Genausdrücke zu berechnen. Damit können Ärzte die Wahrscheinlichkeit für Krebs, Herzinfarkte oder andere Erbkrankheiten vorhersagen.
- Datenvorverarbeitung: Der kNN-Algorithmus kann fehlende Werte in Datensätzen durch Schätzung ermitteln.
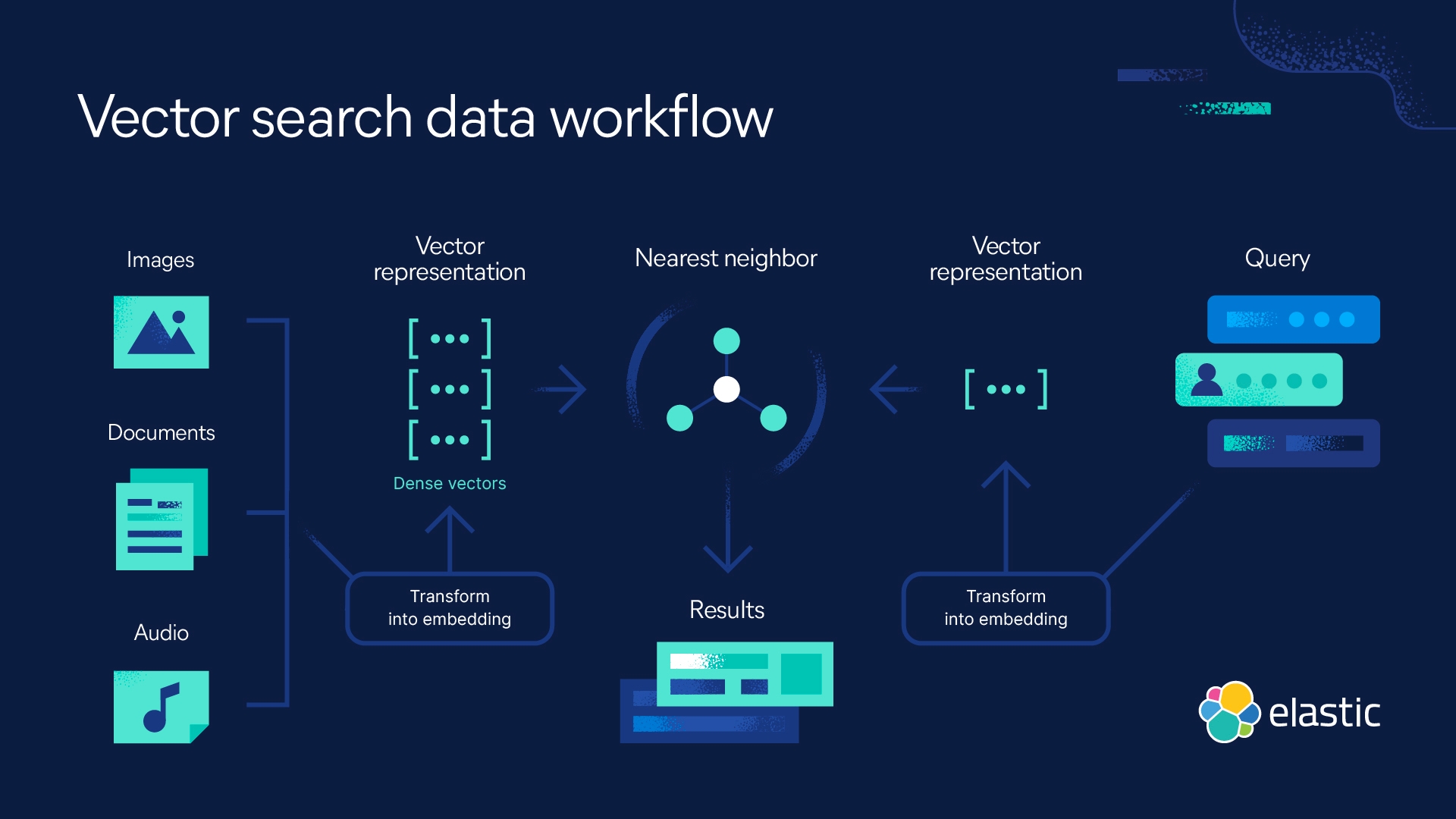
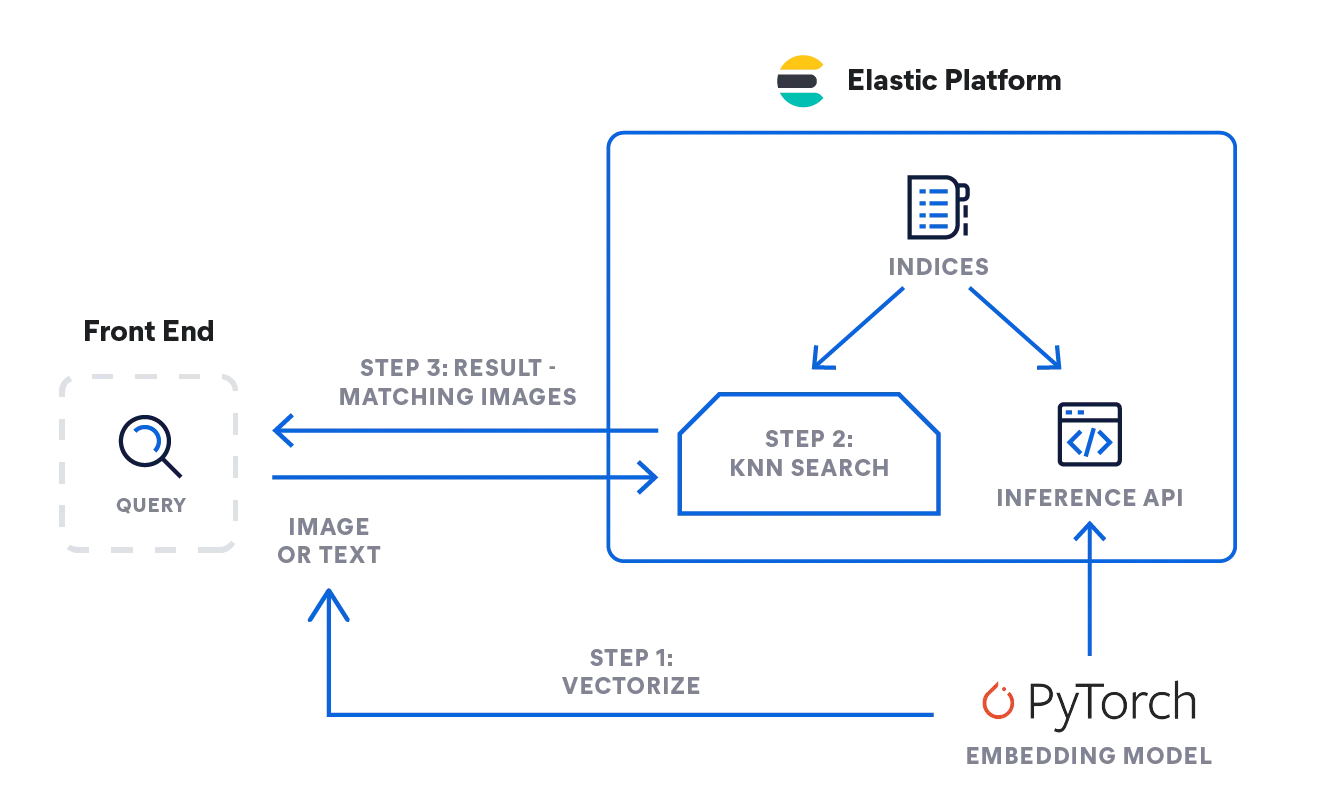
kNN-Suche mit Elastic
Mit Elasticsearch können Sie Ihre eigene kNN-Suche implementieren. Zwei Methoden werden unterstützt: geschätzte kNN-Suche und exakte Brute-Force-kNN-Suche. Sie können die kNN-Suche für Funktionen wie Ähnlichkeitssuche, Relevanzrangfolge auf Basis von NLP-Algorithmen sowie für Produktempfehlungen und Empfehlungs-Engines einsetzen.
FAQ zum k-Nearest-Neighbor-Algorithmus
Wann macht es Sinn, kNN einzusetzen?
Mit kNN können Sie Vorhersagen anhand der Ähnlichkeit treffen. Daher können Sie kNN für Relevanzrangfolgen zusammen mit Algorithmen für natürliche Sprachverarbeitung sowie für Funktionen wie Ähnlichkeitssuche, Empfehlungs-Engines oder Produktempfehlungen einsetzen. kNN ist hilfreich, wenn Ihr Datensatz relativ klein ist.
Ist kNN ein beaufsichtigter oder unbeaufsichtigter Machine-Learning-Algorithmus?
kNN ist ein beaufsichtigter Machine-Learning-Algorithmus. Er wird mit einer Reihe von Daten gefüttert, die gespeichert und erst zum Abfragezeitpunkt verarbeitet werden.
Was bedeutet kNN?
kNN ist der k-Nearest-Neighbor-Algorithmus (k-nächster-Nachbar), wobei „k“ die Anzahl der nächsten Nachbarn ist, die bei der Analyse berücksichtigt werden.
Fußnoten
- Silverman, B.W., & Jones, M.C. (1989). E. Fix and J.L Hodes (1951): An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation: Commentary on Fix and Hodges (1951). International Statistical Institute (ISI) / Revue Internationale de Statistique,57(3), 233–238. https://doi.org/10.2307/1403796
- T. Cover and P. Hart, "Nearest neighbor pattern classification," in IEEE Transactions on Information Theory, vol. 13, no. 1, pp. 21-27, January 1967, doi: 10.1109/TIT.1967.1053964. https://ieeexplore.ieee.org/document/1053964/authors#authors
- K-Nearest Neighbors Algorithm: Classification and Regression Star, History of Data Science, Accessed: 10/23/2023, https://www.historyofdatascience.com/k-nearest-neighbors-algorithm-classification-and-regression-star/